Number of Islands

Leet code: 200. Number of Islands Difficulty: Medium

Problem Definition

Given an m x n 2D binary grid grid which represents a map of '1's (land) and '0's (water), return the number of islands.

An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

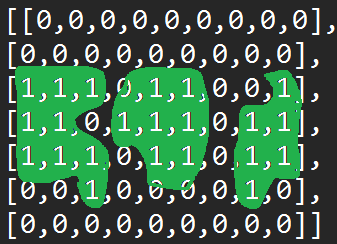
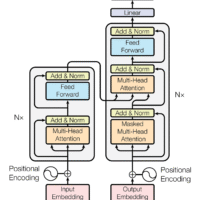
If You are not familiar with graph traversal algorithms this problem might leave you stomped for days and even if you managed to get a solution going it could be really inefficient and time out. Moreover, looking at the problem it is even hard to in-vision a brute force approach to solving it.

What is this special algorithm that will help us solve this problem? first we will need to form a better understanding of the what the solution may look like then form this we can gain insights into the solutions we can employ.

Brainstorming solutions:

The main principle is that when we visit an island; lets say we land on a 1 then we know that this is an island and any other 1’s we see that is compliant with the navigation rules (vertically and horizontally) is part of that island.

• When we visit a unit of land
• define the area of that land
• add to the number of land
• when visit another land that is not in the area
• repeat steps 1, 2 and 3
• return the number of islands

Take a simpler grid:

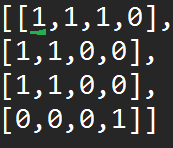
We are starting at (0,0) and we want to define the area contain 1’s based on the navigation rule, where 1’s found vertically and horizontal are considered part of the same island. As show in the image below.

So we follow the navigation rules and find the other lands. Now we repeat this for the newly discovered lands.

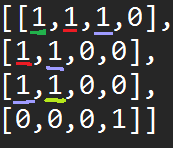
This is the finished outcome of this traversal. We see that we have successfully defined the area of the land.

We can notice that this has sort of a radial effect, where we propagate through all the connected lands. we think of these other lands as the neighbours of the initial land we encountered. Now we can see that this is just a graph problem.

With this graph problem we are trying to find the number of dis-connected graphs in the adjacency matrix.

We can use a graph traversal algorithm to solve this problem, by taking the rule compliant land as neighbours of the initial land and finding all the connected lands using either DFS or BFS. In this case I will be using DFS.

DFS Solution:

def solution(grid):
    num_islands = 0
    visited = set()

    def dfs(i,j):
        if ( i not in range(len(grid)) or 
            j not in range(len(grid[0])) or
            grid[i][j] == '0' or
            (i,j) in visited):
            return

        visited.add((i,j))
        # visit the neighbours
        dfs(i+1, j)
        dfs(i-1, j)
        dfs(i, j+1)
        dfs(i, j-1)


    for i in range(len(grid)):
        for j in range(len(grid[0])):
            if grid[i][j] != '0' and (i,j) not in visited:
                num_islands += 1
                # define the area of the land
                dfs(i,j) 

    return num_islands

BSF Solution:

def solution(grid):
    num_islands = 0 
    visited = set()
    
    def bfs(i,j):
        q = []
        visited.add((i,j))
        q.append((i,j))
        directions = [[1,0],[-1,0],[0,-1],[0,1]]

        while q:
            r,c = q.popleft()
            for dr, dc in directions:
                nr, nc = r+dr, c+dc
                if (nr in range(len(grid)) and
                    nc in range(len(grid[0]) and
                    grid[nr][nc] != '0' and 
                    (nr, nc) not in visited):
                    visited.add((nr,nc))
                    q.append((nr,nc))
 
    for i in range(len(grid)):
        for j in range(len(grid[0])):
            if grid[i][j] != '0' and (i,j) not in visited:
                num_islands += 1
                bfs(i,j)

    return num_islands